
Keine Ahnung von der Principal Component Analysis?
Dann brauchst Du dieses Tutorial!
Hier ist die visuelle Erklärung, wie PCAs funktionieren!
Was ist die PCA?
Die PCA, Principal Component Analysis, zu Deutsch Hauptkomponentenanalyse vereinfacht, strukturiert und visualisiert statistische Datensätze. Ich empfehle Dir diese Data Science Tutorials, um den Einstieg in PCA zu erleichtern. Die PCA gehört zu der multivariaten Statistik, die mehreren statistischen Variablen gleichzeitig analysiert.
Die PCA nutzt die Linearkombination (z. B. 18 = 6 * 2 + 3 * 2), welche mehrere statistischen Merkmale zu den Hauptkomponenten zusammenführt.
Anwendung in der Realität – Für was brauche ich die PCA?
Wer braucht den PCAs? Was bringen die Hauptkomponenten? Diese Berufe lieben PCAs …
- Banker nutzen die PCAs für das Risiko-Management von Ihren Zinsderivaten. Ein Derivat sichert ein Risiko ab und läuft auf einem Basiswert (in diesem Fall der Zins).
- Neurologen untersuchen mithilfe von PCAs Gehirn-Neuronen auf die Reaktionsfähigkeit der intelligenten Zellen.
- Volkswirte untersuchen mit einer PCA eine Volkswirtschaft, weil die Volkswirte oft mit sehr vielen Datensätze und Merkmalen arbeiten müssen.
- Chemiker analysieren damit Proben von Substanzen.
Beispiel für Anwendung von PCA
Die multivariate Statistik analysiert statistische Modelle mit vielen verschiedenen Variablen (Merkmalen). Am besten kann ich die Funktionsweise der PCA an dem Beispiel „Kraftwagen“ (alles, was auf der Straße rollt) erklären.
Einen Kraftwagen beschreiben verschiedene kontinuierliche Merkmale, die die PCA gruppiert:
- Länge
- Breite
- Höhe
- Sitzplätze (nur in Ganzzahlen)
- Gewicht
- Pferdestärken (gemessen in Kilowattstunden)
- Hubraum
- Lastgewicht
Die PCA analysiert die statischen Merkmale und sucht nach ähnlichen Variablen, die im (direkten) Zusammenhang stehen. Die PCA fasst z. B. Länge, Breite, Höhe zu „Größe“ und Pferdestärken, Hubraum und Lastengewicht zu „Leistung“ zusammen.
Auf deutschen Straßen rollen z. B. diese Kraftwagen:
| Typ | Größe | Leistung |
| Kleinauto | Klein | Gering |
| SUV | Mittel | Hoch |
| Rennauto | Klein | Sehr hoch |
| Lastkraftwagen | Sehr groß | Sehr hoch |
Anstatt Dir alle Variablen anzusehen, kannst Du Dir die wesentlichen Gruppenwerte (die Hauptkomponenten) miteinander vergleichen.
Wie funktioniert eine Hauptkomponentenanalyse?
Ziel der Principal Component Analysis
Bevor Du in das Mathematische abtauchst, solltest Du das Ziel und Grund der Berechnungen kennen. Du möchtest mit der PCA die Variablen in einem Datensatz reduzieren.
Du bildest verallgemeinerte Merkmalsgruppen und trennst die Daten in die Hauptkomponenten auf. Mit den Hauptkomponenten willst Du die Streuung besser erklären und hervorsagen können.
Voraussetzung für Principal Component Analysis
Die PCAs braucht Intervall skalierte Skalen (kein ordinalen oder nominalen). Beispiele hierfür sind
- Zeit
- Gewicht
- Geschwindigkeit
- Höhe
- …
Die Daten für eine erfolgreiche PCA sollten keine hohen Fehl-Varianzen aufzeigen. Du brauchst möglichst exakte Messungen ohne Fehler.
Grafische Lösung als Principal Component Analysis
Das Statistikprogramm legt Dir einen Vektor (die Hauptkomponente) entlang des längsten Durchmessers der Punktewolke. Die zweite Hauptkomponente steht orthogonal zu der ersten Achse. Die Punktewolke sieht dann wie eine zermatschte Kidneybohne aus J
5 Schritte für die Principal Component Analysis
Zuerst verschaffst Du Dir mit einem Streudiagramm einen Überblick (2D und 3D). In der Data Science / Statistik solltest Du Dir vor Augen führen, wie Dein Datensatz visuell aussieht.
Du kannst Fehler und Muster leichter erkennen und überprüfen, ob Deine Ergebnisse Sinn ergeben!
Diese Schritte brauchen wir, um von 40 Merkmale auf einige wenige Hauptkomponenten zu kommen.
- Standardisierung der Skalen
- Berechnung der Kovarianz-Matrix
- Umwandlung in die Eigenwerte-Vektoren
- Features Vector ermitteln
- Vektor mit Datensatz verknüpfen
# 1 Skalen standardisieren
Das Beispiel analysiert Volksnationen – daraus ergibt sich folgende Herausforderung:
| Merkmal | Minimum (ohne Ausreißer) | Maximum (ohne Ausreißer) |
| Alter (Jahre) | 0 | 110 |
| Nettohaushaltseinkommen (€) | 400 | 200.000 |
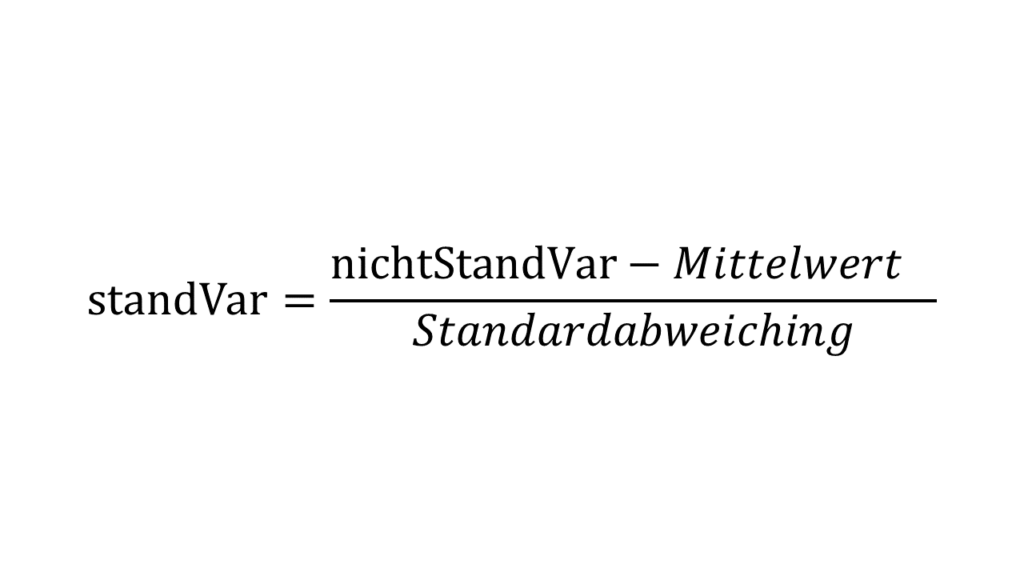
Die Standardisierung versucht die Steuerung auf einen Wertebereich von -1 und 1 abzubilden, um diese besser vergleichen zu können. Du kannst mit der folgenden Formel, die Werte standardisieren:
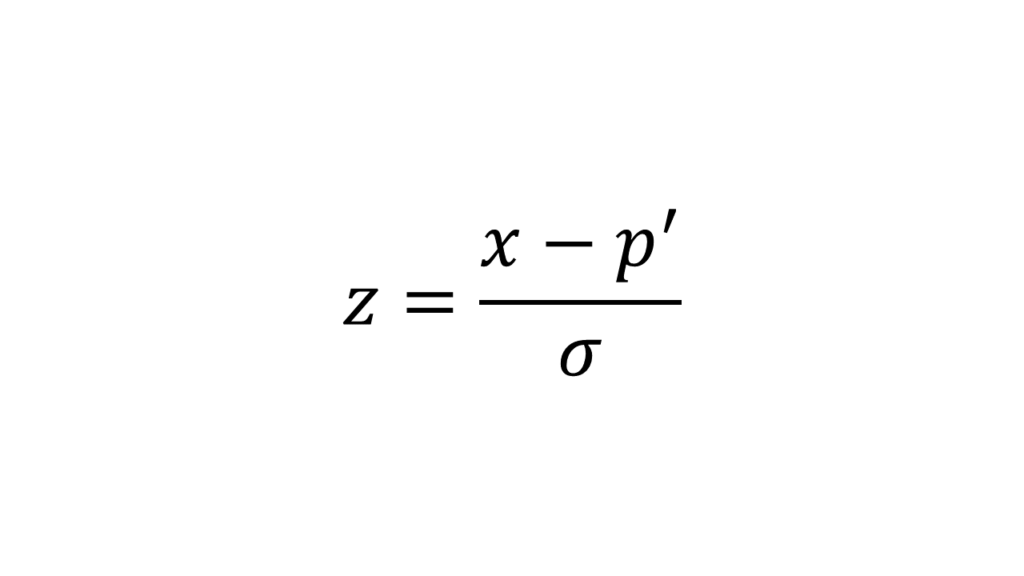
Wenn Du die Formel programmatisch umsetzen willst, empfehle ich Dir den StandarScaler von scikit learn zu verwenden. Die Python Bibliothek bietet eine Vielzahl an Funktionen an, die Du in Deine Statistik / Künstliche Intelligenz Projekten verwenden kannst. Lese das Python Tutorial oder das KI Tutorial, um besser die Materie zu verstehen.
# 2 Kovarianz-Matrix berechnen
Der Computer berechnet in dem nächsten Schritt die Kovarianzen aller Möglichkeiten (x, y und z in 2-Paaren).
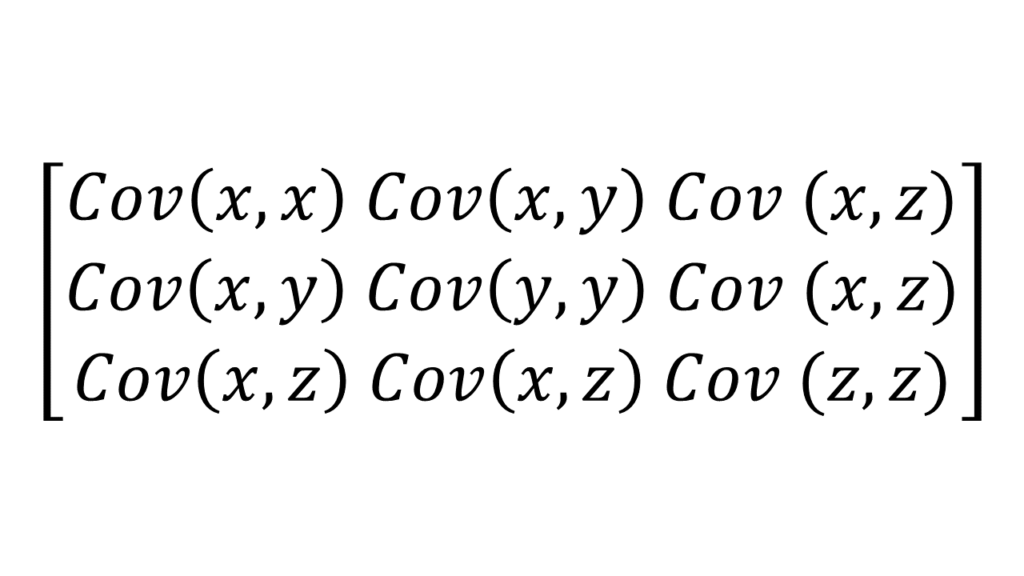
Die Kovarianz ermittelt die Korrelation zweier Merkmale. Als Ergebnis kommt entweder …
| Werte | Bedeutung |
| Korvarianz @ 0 | keine Korrelation, keine Abhängigkeit |
| Korvarianz stark positiv | Korrelation bzw. Abhängigkeit vorhanden |
| Korvarianz negativ positiv | Korrelation bzw. Abhängigkeit vorhanden |

In Python kannst Du diese Funktion nutzen, die auf numpy Bibliothek von Python aufbaut. Das Numpy-Paket hilft Dir, große Tabellen und Arrays intelligent zu verwalten und damit zu rechnen.
# 3 Eigenvektoren berechnen
Wenn Du die Kovarianz-Matrix berechnet hast, berechnest Du den Eigenwert. Dazu ziehst Du die Einheitsmatrix (Variable y) von der Kovarianz-Matrix ab und berechnest über Kreuz die Eigenwerte nach der Additionsmethode.
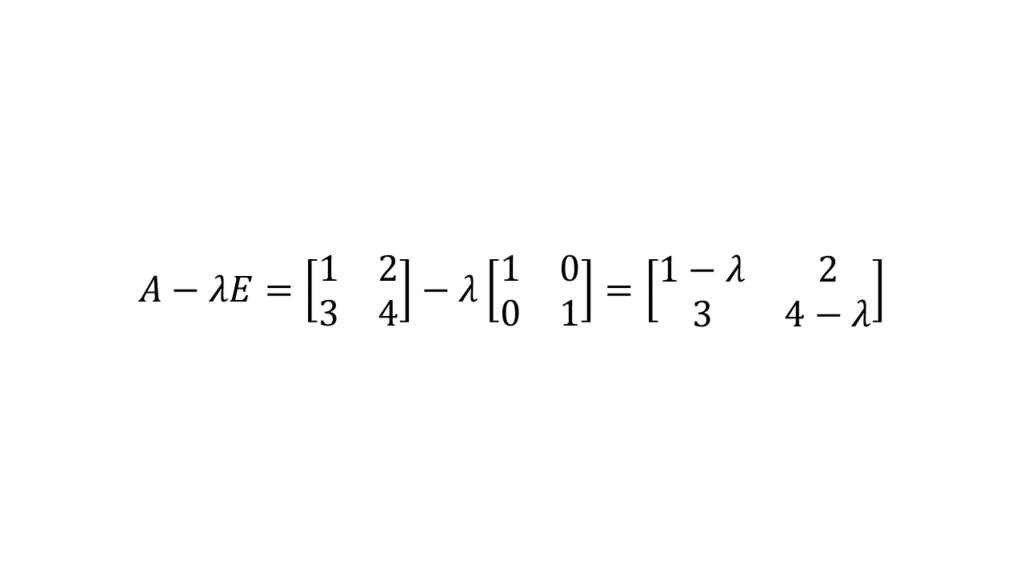
Ein großer Buchstabe in einer Formel bedeutet, dass es sich um eine Matrix handelt.
Eine Einheitsmatrix ist eine n x n Matrix, die mit Nullen aufgefüllt und nur in der Diagonalen 1 als Werte enthält.
Die Variabel ermittelst Du mit etwas Algebra …
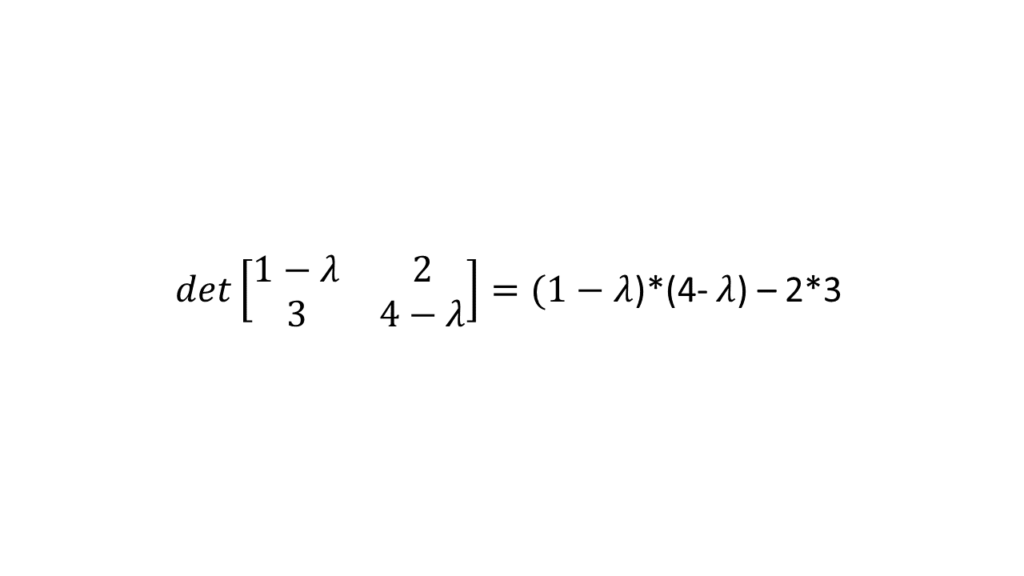
Im Computer kannst Du den Eigenwert auch mit dem numpy-Paket berechnen. Schaue Dir dazu die Erklärung der Uni-Münster an:
import numpy
import numpy.linalg as linalg
A = numpy.random.rand(100,100)
ew,ev = linalg.eig(A)# 4 Features Vektor ermitteln
Der Features Vektor ist der Vektor, der aus den Eigenvektoren besteht. Du schreibst die Eigenwerte in einen Vektor! Schreibe die Eigenvektoren untereinander und Du hast den fertigen Features Vektor.
# 5 Vektor mit Datensatz verknüpfen
Im letzten Schritt führst Du eine Matrizen-Multiplikation von dem Feature Vektor und dem standardisierten Datensatz durch, der transponiert (diagonal geflippt ist). Mit diesem Trick passt Du den Datensatz den Vektoren an.
Bei einer Matrizen-Multiplikation multiplizierst Du jeden Wert in einer Reihe mit dem 1. Wert in Deinem Vektor … und Du arbeitest Dich Reihe für Reihe und Vektorstelle für Vektorstelle durch die Matrix durch.
Wenn eine Matrix transponiert ist, dann tauschst Du die Spalten mit den Reihen. Statt die Werte von links nach rechts auszuschreiben, füllst Du die Matrix von oben links nach unten links auf. Oft nutzen Mathematiker ein hochgestelltes T, um die Transponierung anzuzeigen.
Ergebnis: Die Hauptkomponente kannst Du für die vereinfachte Analyse Deiner Datensätze verwenden.
PCA Anwendung in Data Science
Die PCA nutzen die Data Scientist für die Daten-Visualisierung. Wenn Du 6 Merkmale hast, musst Du 15 Diagramme (Binomialkoeffizienten à 6 über 2) erstellen.
Als Data Scientist verlierst Du den Überblick. Du wünschst Dir nur 1 2D oder 3D Diagramm, welches klare Trennungen aufzeigt!
Aufpassen: Die PCA ist Dir keine Hilfe bei der Klassifikation, weil die mathematische Methode die Komplexität eines Modells reduziert. Die PCA hilft der den Überblick zu behalten
Tipp: Kennst Du schon die Support Vector Machine? – das ist ultra gut brauchbar in der Data Science!
